TL;DR?
WHAT IS BACKWARD FADING?
'In backward faded worked examples, students are required to try to find a solution in the last step on problem 1, the last two steps on problem 2, and so on. In other words, students are required to continue the steps given to solve the problem.'
Omitting an additional step in each worked example allows pupils to build up to independent problem solving, having seen (and worked through) each solution step multiple times.
This is in contrast to 'forward fading' where the fading occurs in the first step on problem 1, the first two steps on problem 2, and so on. In this setup, pupils are required to fill in the missing steps in the solution.
Omitting an additional step in each worked example allows pupils to build up to independent problem solving, having seen (and worked through) each solution step multiple times.
This is in contrast to 'forward fading' where the fading occurs in the first step on problem 1, the first two steps on problem 2, and so on. In this setup, pupils are required to fill in the missing steps in the solution.
why is backward fading beneficial?
According to Cognitive Load Theory, faded examples can assist pupils in developing more advanced problem solving skills. The gradual introduction of parts for pupils to complete lessens the cognitive demand of the task, enabling pupils to attend to a specific element of the problem solving procedure and develop strategies across the worked examples.
Backward fading is preferable to forward fading as the cognitive demand of the latter steps in problem solving solutions are typically lower than earlier steps. As a result the steps with a higher cognitive demand are shown multiple times (when using backward fading) before pupils are expected to complete this step themselves.
Backward fading is preferable to forward fading as the cognitive demand of the latter steps in problem solving solutions are typically lower than earlier steps. As a result the steps with a higher cognitive demand are shown multiple times (when using backward fading) before pupils are expected to complete this step themselves.
WHAT ARE PROMPTS?
There are 'significant learning gains' of backward fading, which can be further built upon by replacing the faded steps with prompts, which you'll find examples of in the resources below.
Prompts direct the attention of the learner to the relevant information in the problem, which helps to foster the development of problem solving skills. Having faded the worked examples, pupils are attending to a limited number of aspects of solving the problem, and so the load imposed on the cognitive ability of the pupil is minimised, enabling pupils to fully process each step of the problem in turn. The best way for pupils to do this is to self-explain each step, but this is inadequately done by the majority of learners.
The use of prompts addresses these failings, making use of the freed up cognitive capacity by asking questions of pupils to aid them in identifying the important parts of the posed problem, as well as their applications within the given context.
Prompts direct the attention of the learner to the relevant information in the problem, which helps to foster the development of problem solving skills. Having faded the worked examples, pupils are attending to a limited number of aspects of solving the problem, and so the load imposed on the cognitive ability of the pupil is minimised, enabling pupils to fully process each step of the problem in turn. The best way for pupils to do this is to self-explain each step, but this is inadequately done by the majority of learners.
The use of prompts addresses these failings, making use of the freed up cognitive capacity by asking questions of pupils to aid them in identifying the important parts of the posed problem, as well as their applications within the given context.
what's out there already?
'Backward fading' is something that I came across in my CPD with Complete Mathematics, and they come up quite regularly when I read a maths book. The problem is that there's not a great lot of detail in these books about what backward fading is, and/or where to find activities which incorporate backward fading.
If you Google 'backward faded examples' you get a return of (as of January 7, 2022) a worksheet from Chris McGrane, and links to research into backward fading. Craig Barton has pages on his web site which give key takeaways from research papers, in case you're interested in reading those, but the key message about backward faded examples is that 'gradually removing the later steps in a multi-step problem brings about significant learning gains' (Atkinson et al, 2003) when compared to example-problem pairs.
If you Google 'backward faded examples' you get a return of (as of January 7, 2022) a worksheet from Chris McGrane, and links to research into backward fading. Craig Barton has pages on his web site which give key takeaways from research papers, in case you're interested in reading those, but the key message about backward faded examples is that 'gradually removing the later steps in a multi-step problem brings about significant learning gains' (Atkinson et al, 2003) when compared to example-problem pairs.
HOW MIGHT YOU USE THE RESOURCES?
The resources are free to use as you wish (obviously), but in many cases my suggestion would be to give pupils 5 minutes in silence to study the worked example and continue to work through the faded examples, following this up with a discussion to identify any misconceptions that have developed. I would progress the discussion through the sheet as far as pupils have worked, before setting them off on the sheet again and then on to a follow up exercise to develop greater levels of fluency.
HOW DO I SUBMIT SOME RESOURCES THAT I'VE PUT TOGETHER?
When I wrote my Increasingly Difficult Questions, I felt that I needed to create them in order to share them. I wanted to be the one who made, uploaded, amended, ... did everything with them.
I was wrong.
I'd like to invite everyone to submit whatever resources they've created, and I'll share them on this page. If you want to use a template, use one of these (three questions on 1-side, four questions on 2-sides, six questions on 1-side, follow-up activities) and email them to d.taylor3142 @ gmail.com (no space, obviously) or DM me on Twitter at @taylorda01.
If you want a 'how-to' video, this might be useful:
I was wrong.
I'd like to invite everyone to submit whatever resources they've created, and I'll share them on this page. If you want to use a template, use one of these (three questions on 1-side, four questions on 2-sides, six questions on 1-side, follow-up activities) and email them to d.taylor3142 @ gmail.com (no space, obviously) or DM me on Twitter at @taylorda01.
If you want a 'how-to' video, this might be useful:
SHOW ME THE RESOURCES!
OK... Here you go...
Number AND RATIO & PROPORTION

Adding and Subtracting Using Fractions
by Dave Taylor
Solutions: a) 39/88, b) 9/20, c) 11/18, d) 8/15
Follow-up Activity: .pdf
Solutions: 29/45, b) 9/10, c) 3/4
by Dave Taylor
Solutions: a) 39/88, b) 9/20, c) 11/18, d) 8/15
Follow-up Activity: .pdf
Solutions: 29/45, b) 9/10, c) 3/4
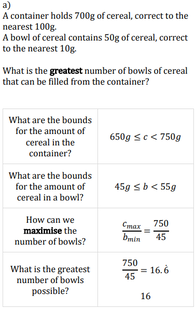
Calculations With Bounds
by Dave Taylor
Solutions: a) 16, b) 15, c) 23
Follow-up Activity: .pdf
Solutions: a) 22, b) lower bound = 17.42 (2 d.p.),
upper bound = 18, c) 300 (to the nearest hundred)
by Dave Taylor
Solutions: a) 16, b) 15, c) 23
Follow-up Activity: .pdf
Solutions: a) 22, b) lower bound = 17.42 (2 d.p.),
upper bound = 18, c) 300 (to the nearest hundred)



Contextual Fractions
by Dave Taylor
Solutions: a) 288m, b) 150g, c) 750ml
Follow-up Activity: .pdf
Solutions: a) 2.4km, b) 40 chocolates, c) 24 biscuits
by Dave Taylor
Solutions: a) 288m, b) 150g, c) 750ml
Follow-up Activity: .pdf
Solutions: a) 2.4km, b) 40 chocolates, c) 24 biscuits

Contextual Lowest Common Multiple
by Dave Taylor
Solutions: a) 10:10, b) 14:30, c) 14:58, d) 13:37
Follow-up Activity: .pdf
Solutions: a) 120 seconds, b) 3 tins of hot dogs and 4 packets of hot dog buns, c) 24 pupils
by Dave Taylor
Solutions: a) 10:10, b) 14:30, c) 14:58, d) 13:37
Follow-up Activity: .pdf
Solutions: a) 120 seconds, b) 3 tins of hot dogs and 4 packets of hot dog buns, c) 24 pupils
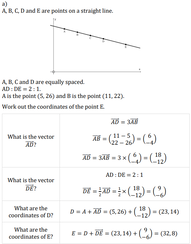
Coordinates and Ratio
by Dave Taylor
Solutions: a) (32,8), b) (29,5), c) (19,12), d) (24,20)
Follow-up Activity: .pdf
Solutions: a) (26, 27.75), b) (14.5, 21), c) (3,0)
by Dave Taylor
Solutions: a) (32,8), b) (29,5), c) (19,12), d) (24,20)
Follow-up Activity: .pdf
Solutions: a) (26, 27.75), b) (14.5, 21), c) (3,0)
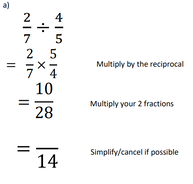
Dividing Fractions
by Bob Jackson
Solutions: a) 5/14, b) 5/14, c) 7/22, d) 3/28, e) 7/8, f) 27/28
by Bob Jackson
Solutions: a) 5/14, b) 5/14, c) 7/22, d) 3/28, e) 7/8, f) 27/28

Electricity Readings
by Dave Taylor
Solutions: a) £73.60, b) £266.38, c) £225.54, d) £144.54
Follow-up Activity: .pdf
Solutions: a) £206.46, b) £312.29, c) £894.52
by Dave Taylor
Solutions: a) £73.60, b) £266.38, c) £225.54, d) £144.54
Follow-up Activity: .pdf
Solutions: a) £206.46, b) £312.29, c) £894.52

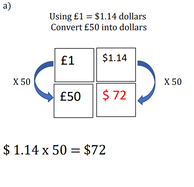
Exchange Rates
by Connor Rollo
Solutions: a) $72, b) £74.56, c) 356.80 Lev, d) £200,
e) 476 Swiss Franc, f) £239.35
by Connor Rollo
Solutions: a) $72, b) £74.56, c) 356.80 Lev, d) £200,
e) 476 Swiss Franc, f) £239.35




Inverse Proportion
by Dave Taylor
Solutions: .png
Follow-up Activity: .pdf
Solutions: a) y = 160/x³, b) y = 3, c) x = 100
by Dave Taylor
Solutions: .png
Follow-up Activity: .pdf
Solutions: a) y = 160/x³, b) y = 3, c) x = 100

Inverse Proportion
by Bob Jackson
Solutions: a) i) P = 28/Q, ii) P = 4, b) i) P = 36/Q, ii) P = 4,
c) i) P = 48/Q, ii) P = 16, d) i) P = 60/Q, ii) P = 4,
e) i) P = 20/Q, ii) P = 2.5, f) i) P = 40/Q, ii) P = 5
by Bob Jackson
Solutions: a) i) P = 28/Q, ii) P = 4, b) i) P = 36/Q, ii) P = 4,
c) i) P = 48/Q, ii) P = 16, d) i) P = 60/Q, ii) P = 4,
e) i) P = 20/Q, ii) P = 2.5, f) i) P = 40/Q, ii) P = 5

Maximum Servings From a Recipe
by Dave Taylor
Solutions: a) 25 biscuits, b) 24 pancakes, c) 10 servings,
d) 4 servings
by Dave Taylor
Solutions: a) 25 biscuits, b) 24 pancakes, c) 10 servings,
d) 4 servings

Money and Coins
by Dave Taylor
Solutions: a) 4 coins, b) 5 coins, c) 4 coins, d) 5 coins
Follow-up Activity: .pdf
Solutions: a) (20p, 5p, 1p, 1p, 1p) or (10p, 10p, 5p, 2p, 1p) or (20p 2p, 2p, 2p, 2p) b) (20p, 5p, 2p, 1p) and (10p, 10p, 5p, 2p, 1p) = 2 ways, c) (50p, 10p, 2p, 1p) = 4 coins
by Dave Taylor
Solutions: a) 4 coins, b) 5 coins, c) 4 coins, d) 5 coins
Follow-up Activity: .pdf
Solutions: a) (20p, 5p, 1p, 1p, 1p) or (10p, 10p, 5p, 2p, 1p) or (20p 2p, 2p, 2p, 2p) b) (20p, 5p, 2p, 1p) and (10p, 10p, 5p, 2p, 1p) = 2 ways, c) (50p, 10p, 2p, 1p) = 4 coins

Money, Percentages and Ratio
by Dave Taylor
Solutions: a) 8 : 3, b) 4 : 3, c) 5 : 3, d) 1 : 2
Follow-up Activity: .png
Solutions: a) 1 : 2, b) 4 : 5, c) 25 : 13, d) 30 : 17
by Dave Taylor
Solutions: a) 8 : 3, b) 4 : 3, c) 5 : 3, d) 1 : 2
Follow-up Activity: .png
Solutions: a) 1 : 2, b) 4 : 5, c) 25 : 13, d) 30 : 17

More Complex Calculation with Bounds
by Dave Taylor
Solutions: a) 20.6, b) 24.2, c) 11, d) 7
Follow-up Activity: .pdf
Solutions: a) 99/61, b) 130/7 ≤ (a-b)/c < 70,
c) 13.95 ≤ ac/(b-c) < 39.29
by Dave Taylor
Solutions: a) 20.6, b) 24.2, c) 11, d) 7
Follow-up Activity: .pdf
Solutions: a) 99/61, b) 130/7 ≤ (a-b)/c < 70,
c) 13.95 ≤ ac/(b-c) < 39.29
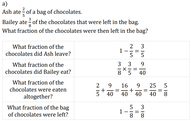
Multiplying Fractions in Context
by Dave Taylor
Solutions: a) 2.5% decrease, b) 32% increase, c) 0.25% decrease, d) 25.44% increase
by Dave Taylor
Solutions: a) 2.5% decrease, b) 32% increase, c) 0.25% decrease, d) 25.44% increase



Percentage Change
by Dee Vijayan
Solutions: a) 25%, b) 20%, c) 12%, d) 10.8% (1d.p.),
e) 20%, f) 25%
by Dee Vijayan
Solutions: a) 25%, b) 20%, c) 12%, d) 10.8% (1d.p.),
e) 20%, f) 25%

Percentage Profit
by Bob Jackson
Solutions: a) 4.76%, b) 57.14%, c) 15.79%, d) 19.05%, e) 17.69%,
f) 26.52%
by Bob Jackson
Solutions: a) 4.76%, b) 57.14%, c) 15.79%, d) 19.05%, e) 17.69%,
f) 26.52%

Proportional Reasoning
by Dave Taylor
Solutions: a) 2 hours 15 minutes, b) 2 hours 15 minutes,
c) 3 hours 45 minutes, d) 2 hours 40 minutes
Follow-up Activity: .pdf
Solutions: a) 1 hour 20 minutes, b) 1 hour 41 minutes,
c) 13 hours 20 minutes
by Dave Taylor
Solutions: a) 2 hours 15 minutes, b) 2 hours 15 minutes,
c) 3 hours 45 minutes, d) 2 hours 40 minutes
Follow-up Activity: .pdf
Solutions: a) 1 hour 20 minutes, b) 1 hour 41 minutes,
c) 13 hours 20 minutes


Rates in Context
by Dave Taylor
Solutions: a) 260 minutes, b) 601 minutes,
c) 68 minutes, d) 93 minutes
Follow-up Activity: .pdf
Solutions: a) 208 minutes, b) 1694 minutes,
c) Machine B
by Dave Taylor
Solutions: a) 260 minutes, b) 601 minutes,
c) 68 minutes, d) 93 minutes
Follow-up Activity: .pdf
Solutions: a) 208 minutes, b) 1694 minutes,
c) Machine B

Ratio, Fractions and Percentages
by Dave Taylor
Solutions: a) 30, b) 26, c) 72, d) 28
Follow-up Activity: .pdf
Solutions: a) 70, b) 155, c) 71
by Dave Taylor
Solutions: a) 30, b) 26, c) 72, d) 28
Follow-up Activity: .pdf
Solutions: a) 70, b) 155, c) 71




Reverse Percentage Decrease
by Dave Taylor
Solutions: a) £16 000, b) £17 000, c) £16 500, d) £16 200
Follow-up Activity: .pdf
Solutions: a) £30 000, b) £399 000, c) £18 500
by Dave Taylor
Solutions: a) £16 000, b) £17 000, c) £16 500, d) £16 200
Follow-up Activity: .pdf
Solutions: a) £30 000, b) £399 000, c) £18 500

Reverse Percentages
by Dave Taylor
Solutions: a) £495, b) £720, c) 750ml
Follow-up Activity: .pdf
Solutions: a) £480, b) £160,000, c) 480g
by Dave Taylor
Solutions: a) £495, b) £720, c) 750ml
Follow-up Activity: .pdf
Solutions: a) £480, b) £160,000, c) 480g

Reverse Percentages Twice
by Dave Taylor
Solutions: a) 90 minutes, b) 60 minutes, c) 80 minutes,
d) 40 minutes
Follow-up Activity: .pdf
Solutions: a) 50 minutes, b) £620, c) $3099.92
by Dave Taylor
Solutions: a) 90 minutes, b) 60 minutes, c) 80 minutes,
d) 40 minutes
Follow-up Activity: .pdf
Solutions: a) 50 minutes, b) £620, c) $3099.92
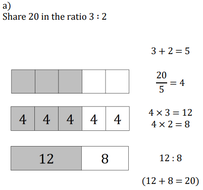
Sharing Amounts in a Ratio
by Dave Taylor
Solutions: a) 12:8, b) 15:5, c) 9:15, d) 6:30, e) 40:16, f) 16:20
by Dave Taylor
Solutions: a) 12:8, b) 15:5, c) 9:15, d) 6:30, e) 40:16, f) 16:20



Using Inverse Proportion
by Dave Taylor
Solutions: a) 4 hours, b) 5 hours, c) 6 hours,
d) 8 hours
Follow-up Activity: .pdf
Solutions: a) 3 hours 12 minutes, b) 6 hours, c) 1280 units
by Dave Taylor
Solutions: a) 4 hours, b) 5 hours, c) 6 hours,
d) 8 hours
Follow-up Activity: .pdf
Solutions: a) 3 hours 12 minutes, b) 6 hours, c) 1280 units
ALGEBRA



Completing The Square
by Chloe Bennett
Solutions: a) (x+2)²+3, b) (x+3)²+8, c) (x+2)²+6,
d) (x+1)²+8, e) (x+4)²+9, f) (x+5)²+47
by Chloe Bennett
Solutions: a) (x+2)²+3, b) (x+3)²+8, c) (x+2)²+6,
d) (x+1)²+8, e) (x+4)²+9, f) (x+5)²+47

Converting Recurring Decimals to Fractions
by Dave Taylor
Solutions: a) 5/9, b) 6/11, c) 49/90, d) 14/33
by Dave Taylor
Solutions: a) 5/9, b) 6/11, c) 49/90, d) 14/33
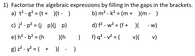

Differentiation From First Principles
by Sam Blatherwick
Solutions: a) f'(x) = 8x, b) f'(x) = 6x², c) f'(x) = x, d) f'(x) = 2x - 1
by Sam Blatherwick
Solutions: a) f'(x) = 8x, b) f'(x) = 6x², c) f'(x) = x, d) f'(x) = 2x - 1

Direct Proportion
by Bob Jackson
Solutions: a) i) P = 5Q, ii) P = 55 , b) i) P = 3Q, ii) P = 33,
c) i) P = 4Q, ii) P = 44, d) i) P = 2.5Q, ii) P = 27.5,
e) i) P = 1.5Q, ii) P = 16.5, f) P = 16Q, ii) P = 176
by Bob Jackson
Solutions: a) i) P = 5Q, ii) P = 55 , b) i) P = 3Q, ii) P = 33,
c) i) P = 4Q, ii) P = 44, d) i) P = 2.5Q, ii) P = 27.5,
e) i) P = 1.5Q, ii) P = 16.5, f) P = 16Q, ii) P = 176



Direct Proportion With Percentage Increase/Decrease
by Dave Taylor
Solutions: a) 44%, b) 125%, c) 33.1%, d) 48.8%
by Dave Taylor
Solutions: a) 44%, b) 125%, c) 33.1%, d) 48.8%

Equation of a Circle
by Dave Taylor
Solutions: a) x²+y²=9, b) x²+y²=25, c) x²+y²=29, d) x²+y²=81
Follow-up Activity: .pdf
Solutions: a) x²+y²=29, not 21, b) Inside, c) (3,8) and (3,-8)
by Dave Taylor
Solutions: a) x²+y²=9, b) x²+y²=25, c) x²+y²=29, d) x²+y²=81
Follow-up Activity: .pdf
Solutions: a) x²+y²=29, not 21, b) Inside, c) (3,8) and (3,-8)

Equation of a Line - Given Gradient and a Point on the Line
by Chloe Bennett
Solutions: a) y = 2x - 7, b) y = 3x + 4, c) y = 3x - 26,
d) y = 8x - 19, e) y = 8x + 29, f) y = -7x - 26
by Chloe Bennett
Solutions: a) y = 2x - 7, b) y = 3x + 4, c) y = 3x - 26,
d) y = 8x - 19, e) y = 8x + 29, f) y = -7x - 26

Equation of a Tangent to a Curve
by Sam Blatherwick
Solutions: a) y = 6x - 4, b) y = 15x - 12,
c) y = 8 - 4x, d) y = (5x + 5)/2
by Sam Blatherwick
Solutions: a) y = 6x - 4, b) y = 15x - 12,
c) y = 8 - 4x, d) y = (5x + 5)/2


Equations of Perpendicular Lines
by Dave Taylor
Solutions: a) y=(-1/2)x+8, b) y=(-1/4)x+4, c) y=17-2x, d) y=-(1/3)x+8
by Dave Taylor
Solutions: a) y=(-1/2)x+8, b) y=(-1/4)x+4, c) y=17-2x, d) y=-(1/3)x+8

The Factor Theorem
by Dave Taylor
Solutions: a) (2x-1)(x-2)(x+4), b) (x-1)(x+1)(x+3),
c) (3x-1)(2x-1)(x+3), d) (3x+1)(x-5)(x+2)
Follow-up Activity: .pdf
Solutions: a) (3x-5)(2x+1)(x+2), b) a = 13, c) x = -3, x = 2 and x = 5
by Dave Taylor
Solutions: a) (2x-1)(x-2)(x+4), b) (x-1)(x+1)(x+3),
c) (3x-1)(2x-1)(x+3), d) (3x+1)(x-5)(x+2)
Follow-up Activity: .pdf
Solutions: a) (3x-5)(2x+1)(x+2), b) a = 13, c) x = -3, x = 2 and x = 5
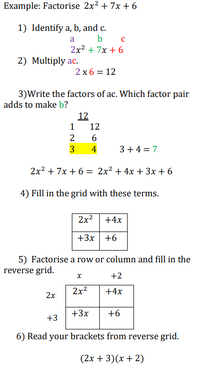
Factorising Quadratics (ac method)
by Chloe Bennett
Solutions: a) (2x+3)(x+2), b) (3x+2)(x+2), c) (5x-3)(x+3),
d) (2x-1)(x+3), e) (3x+5)(x+4), f) (3x-4)(x+4)
by Chloe Bennett
Solutions: a) (2x+3)(x+2), b) (3x+2)(x+2), c) (5x-3)(x+3),
d) (2x-1)(x+3), e) (3x+5)(x+4), f) (3x-4)(x+4)
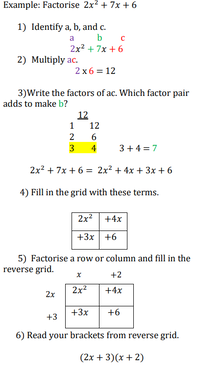
Factorising Quadratics (grid method)
by Chloe Bennett
Solutions: a) (2x+3)(x+2), b) (3x+2)(x+2), c) (5x-3)(x+3),
d) (2x-1)(x+3), e) (3x+5)(x+4), f) (3x-4)(x+4)
by Chloe Bennett
Solutions: a) (2x+3)(x+2), b) (3x+2)(x+2), c) (5x-3)(x+3),
d) (2x-1)(x+3), e) (3x+5)(x+4), f) (3x-4)(x+4)


Forming Equations and Ratio
by Dave Taylor
Solutions: a) 1.5, b) 2.5, c) 3.2, d) 2
Follow-up Activity: .pdf
Solutions: a) 4, b) 2.8, c) 72
by Dave Taylor
Solutions: a) 1.5, b) 2.5, c) 3.2, d) 2
Follow-up Activity: .pdf
Solutions: a) 4, b) 2.8, c) 72

Inverse Proportion
by Bob Jackson
Solutions: a) i) P = 28/Q, ii) P = 4, b) i) P = 36/Q, ii) P = 4,
c) i) P = 48/Q, ii) P = 16, d) i) P = 60/Q, ii) P = 4,
e) i) P = 20/Q, ii) P = 2.5, f) i) P = 40/Q, ii) P = 5
by Bob Jackson
Solutions: a) i) P = 28/Q, ii) P = 4, b) i) P = 36/Q, ii) P = 4,
c) i) P = 48/Q, ii) P = 16, d) i) P = 60/Q, ii) P = 4,
e) i) P = 20/Q, ii) P = 2.5, f) i) P = 40/Q, ii) P = 5


nth Term of Arithmetic/Linear Sequences
by Kieran McConville
Solutions: E) 2n + 3, 1) 4n - 1, 2) 3n + 4, 3) 5n + 2, 4) 3n - 2,
5) 2n + 5
by Kieran McConville
Solutions: E) 2n + 3, 1) 4n - 1, 2) 3n + 4, 3) 5n + 2, 4) 3n - 2,
5) 2n + 5

nth Term of a Quadratic Sequence
by Dave Taylor
Solutions: a) 2n²+3n+5, b) n²+3n+2, c) 4n²+2n-5, d) 2n²-2n+9
by Dave Taylor
Solutions: a) 2n²+3n+5, b) n²+3n+2, c) 4n²+2n-5, d) 2n²-2n+9

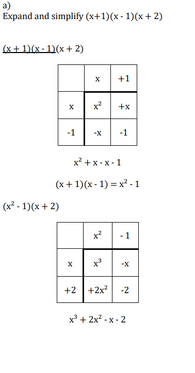

Quadratic Sequences
by Ranjit Kaur and Tara Atefi, St Paul's School for Girls
Solutions: a) 3n²+2n+5, b) 6n²+7n+1, c) 2n²+3n-4, d) n²+5n+3,
e) 5n²+3n-2, f) 7n²+3n+8, g) 9n²+2n-4, h) an²+bn+c
by Ranjit Kaur and Tara Atefi, St Paul's School for Girls
Solutions: a) 3n²+2n+5, b) 6n²+7n+1, c) 2n²+3n-4, d) n²+5n+3,
e) 5n²+3n-2, f) 7n²+3n+8, g) 9n²+2n-4, h) an²+bn+c


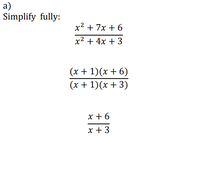

Solving Linear Equations with One Bracket (A)
by Zoe Nye
Solutions: a) x = 4/3, b) x = 5/2, c) x = 23/3, d) x = 6/5,
e) x = 47/5, f) x = 7/3
by Zoe Nye
Solutions: a) x = 4/3, b) x = 5/2, c) x = 23/3, d) x = 6/5,
e) x = 47/5, f) x = 7/3

Solving Linear Equations with One Bracket (B)
by Zoe Nye
Solutions: a) x = 5, b) x = 1, c) x = 18, d) x = -1,
e) x = 12, f) x = 4
by Zoe Nye
Solutions: a) x = 5, b) x = 1, c) x = 18, d) x = -1,
e) x = 12, f) x = 4

Solving Linear Equations with Brackets
by Dee Vijayan
Solutions: a) x = 5, b) x = 13, c) x = 18, d) x = -1,
e) x = 12, f) x = 4
by Dee Vijayan
Solutions: a) x = 5, b) x = 13, c) x = 18, d) x = -1,
e) x = 12, f) x = 4
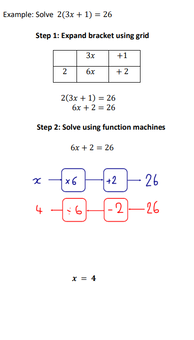
Solving Linear Equations with Brackets
by Chloe Bennett
Solutions: Example) x = 4, a) x = 2, b) x = 3,
c) x = 7, d) x = 5, e) x = 3
by Chloe Bennett
Solutions: Example) x = 4, a) x = 2, b) x = 3,
c) x = 7, d) x = 5, e) x = 3

Solving Linear Equations with Unknowns on Both Sides
by Dee Vijayan
Solutions: a) x = -1, b) x = -4, c) x = 7, d) x = -8,
e) x = -5, f) x = -7
by Dee Vijayan
Solutions: a) x = -1, b) x = -4, c) x = 7, d) x = -8,
e) x = -5, f) x = -7

Solving Linear Equations with Unknowns on Both Sides
by Richard Dare
Solutions: 1) x = 2, 2) x = 2, 3) x = 7, 4) x = 8, 5) x = 8,
6) x = 2, 7) x = 7, 8) x = 4
by Richard Dare
Solutions: 1) x = 2, 2) x = 2, 3) x = 7, 4) x = 8, 5) x = 8,
6) x = 2, 7) x = 7, 8) x = 4
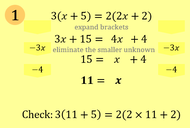
Solving Linear Equations with Unknowns on Both Sides (with Brackets)
by Richard Dare
Solutions: 1) x = 11, 2) x = 2, 3) x = 4, 4) x = 5,
5) x = 3, 6) x = -7, 7) x = 9, 8) x = 3, 9) x = 5, 10) x = 4,
11) x = -4, 12) x = -2
by Richard Dare
Solutions: 1) x = 11, 2) x = 2, 3) x = 4, 4) x = 5,
5) x = 3, 6) x = -7, 7) x = 9, 8) x = 3, 9) x = 5, 10) x = 4,
11) x = -4, 12) x = -2
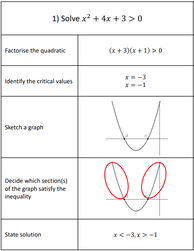
Solving Quadratic Inequalities
by Paul Rochester
Solutions: 1) x < -3, x > 1, 2) 5 < x < 7, 3) -3 ≤ x ≤ 8,
4) x ≤ 3, x ≥ 4, 5) -4 < x < 5, 6) x ≤ -9, x ≥ -7, 7) x < -1, x > 9,
8) -3 < x < 9
by Paul Rochester
Solutions: 1) x < -3, x > 1, 2) 5 < x < 7, 3) -3 ≤ x ≤ 8,
4) x ≤ 3, x ≥ 4, 5) -4 < x < 5, 6) x ≤ -9, x ≥ -7, 7) x < -1, x > 9,
8) -3 < x < 9

Solving Simultaneous Equations
by Alex Hughes
Solutions: a) x = 2, y = 14, b) x = 6, y = 24, c) x = 5, y = 10, d) x = 4, y = 12, e) x = 10, y = 20
a) x = 5, y = 1, b) x = 1, y = 2, c) x = 8, y = 3, d) x = 4, y = 3, e) x = 1, y = -2
by Alex Hughes
Solutions: a) x = 2, y = 14, b) x = 6, y = 24, c) x = 5, y = 10, d) x = 4, y = 12, e) x = 10, y = 20
a) x = 5, y = 1, b) x = 1, y = 2, c) x = 8, y = 3, d) x = 4, y = 3, e) x = 1, y = -2
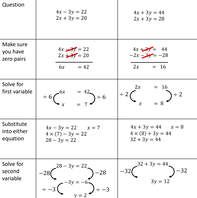
Solving Simultaneous Equations by Elimination
by by Ranjit Kaur and Tara Atefi, St Paul's School for Girls
Equal Coefficients
Solutions: a) x = 7, y = 2, b) x = 8, y = 4, c) x = 5, y = 2,
d) x = 6, y = 3, e) x = 9, y = 5, f) x = 7, y = 4, g) x = 10, y = 8,
h) x = 9, y = 6
Non-equal Coefficients
Solutions: a) x = 1, y = 4, b) x = 5, y = 2, c) x = 1, y = 3, d) x = 5, y = 4, e) x = 5, y = 1,
f) x = 7, y = 3, g) x = 4, y = 3, h) x = 5, y = 2, i) x = 3, y = 4, j) x = 2, y = 4, k) x = -2, y = -1,
l) x = 7, y = 6
Using Algebra Discs
Solutions: a) x = 7, y = 2, b) x = 8, y = 4, c) x = 5, y = 2, d) x = 6, y = 3, e) x = 9, y = 5,
f) x = 7, y = 4, g) x = 10, y = 8, h) x = 9, y = 6
by by Ranjit Kaur and Tara Atefi, St Paul's School for Girls
Equal Coefficients
Solutions: a) x = 7, y = 2, b) x = 8, y = 4, c) x = 5, y = 2,
d) x = 6, y = 3, e) x = 9, y = 5, f) x = 7, y = 4, g) x = 10, y = 8,
h) x = 9, y = 6
Non-equal Coefficients
Solutions: a) x = 1, y = 4, b) x = 5, y = 2, c) x = 1, y = 3, d) x = 5, y = 4, e) x = 5, y = 1,
f) x = 7, y = 3, g) x = 4, y = 3, h) x = 5, y = 2, i) x = 3, y = 4, j) x = 2, y = 4, k) x = -2, y = -1,
l) x = 7, y = 6
Using Algebra Discs
Solutions: a) x = 7, y = 2, b) x = 8, y = 4, c) x = 5, y = 2, d) x = 6, y = 3, e) x = 9, y = 5,
f) x = 7, y = 4, g) x = 10, y = 8, h) x = 9, y = 6
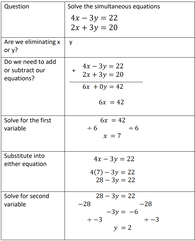
Solving Simultaneous Equations with Equal Coefficients
by Chloe Bennett
Solutions: 1. x = 7, y = 2,
2. x = 8, y = 4,
3. y = 5, x = 2
4. y = 6, x = 3
5. x = 7, y = 4
6. x = 10, y = 8
by Chloe Bennett
Solutions: 1. x = 7, y = 2,
2. x = 8, y = 4,
3. y = 5, x = 2
4. y = 6, x = 3
5. x = 7, y = 4
6. x = 10, y = 8

Solving Simultaneous Equations with a Circle (Substitution)
by Dave Taylor
Solutions: a) x = -5, y = -3 and x = 3, y = 5,
b) x = 4, y = 1 and x = -1, y = -4,
c) x = 7, y = 8 and x = -6 , y = -5,
d) x = 6, y = 1 and x = -1, y = -6
by Dave Taylor
Solutions: a) x = -5, y = -3 and x = 3, y = 5,
b) x = 4, y = 1 and x = -1, y = -4,
c) x = 7, y = 8 and x = -6 , y = -5,
d) x = 6, y = 1 and x = -1, y = -6
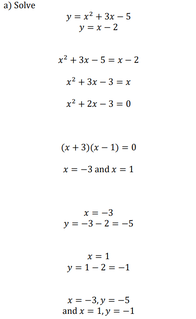
Solving Simultaneous Equations with a Quadratic (Equality)
by Dave Taylor
Solutions: a) x = -3, y = -5 and x = 1, y = -1,
b) x = -2, y = -3 and x = 1, y = 0,
c) x = -1.5, y = -3.5 and x = 2 , y = 7,
by Dave Taylor
Solutions: a) x = -3, y = -5 and x = 1, y = -1,
b) x = -2, y = -3 and x = 1, y = 0,
c) x = -1.5, y = -3.5 and x = 2 , y = 7,
GEOMETRY
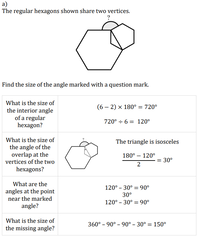
Angles in Regular Polygons
by Dave Taylor
Solutions: a) 150°, b) 72°, c) 135°, d) 162°
Follow-up Activity: .pdf
Solutions: a) 228°, b) 72°, c) 20°
by Dave Taylor
Solutions: a) 150°, b) 72°, c) 135°, d) 162°
Follow-up Activity: .pdf
Solutions: a) 228°, b) 72°, c) 20°
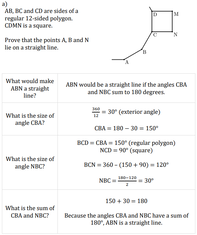

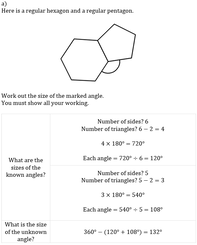
Angles in Regular Polygons at a Point
by Dave Taylor
Solutions: a) 132°, b) 105°, c) 76°, d) 81°
Follow-up Activity: .pdf
Solutions: a) 27°, b) 36°, c) 150°
by Dave Taylor
Solutions: a) 132°, b) 105°, c) 76°, d) 81°
Follow-up Activity: .pdf
Solutions: a) 27°, b) 36°, c) 150°
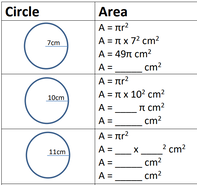
Area of a Circle
by Alex Hughes
Solutions: a) 153.94cm², b) 314.16cm², c) 380.13cm², d) 50.27cm², e) 201.06cm², f) 50.27cm², g) 113.10cm²
by Alex Hughes
Solutions: a) 153.94cm², b) 314.16cm², c) 380.13cm², d) 50.27cm², e) 201.06cm², f) 50.27cm², g) 113.10cm²
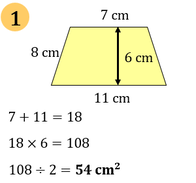
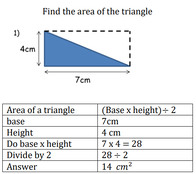
Area of a Triangle
by Dee Vijayan
Solutions: a) 14cm², b) 22.5cm², c) 16cm², d) 15.75cm²,
e) 10cm², f) 31cm²
by Dee Vijayan
Solutions: a) 14cm², b) 22.5cm², c) 16cm², d) 15.75cm²,
e) 10cm², f) 31cm²
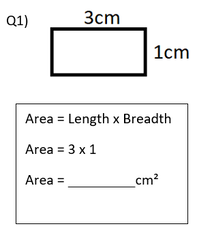

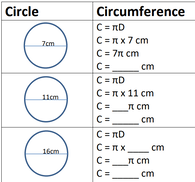
Circumference of a Circle
by Alex Hughes
Solutions: a) 21.99cm, b) 34.56cm, c) 50.27cm, d) 12.57cm,
e) 21.99cm, f) 50.27cm, g) 56.55cm
by Alex Hughes
Solutions: a) 21.99cm, b) 34.56cm, c) 50.27cm, d) 12.57cm,
e) 21.99cm, f) 50.27cm, g) 56.55cm
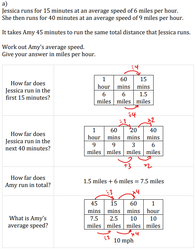
Combining Average Speeds
by Dave Taylor
Solutions: a) 10mph, b) 12mph, c) 11.25mph, d) 8mph
Follow-up Activity: .pdf
Solutions: a) 21mph, b) 20mph, c) 20.3km/h (to 1d.p.)
by Dave Taylor
Solutions: a) 10mph, b) 12mph, c) 11.25mph, d) 8mph
Follow-up Activity: .pdf
Solutions: a) 21mph, b) 20mph, c) 20.3km/h (to 1d.p.)
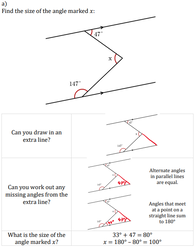
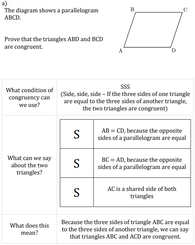

Contextual Area of a Semi-Circle
by Dave Taylor
Solutions: a) £142.20, b) £74.00, c) £45.00, d) £40.80
Follow-up Activity: .pdf
Solutions: a) £17.10, b) £67.80
by Dave Taylor
Solutions: a) £142.20, b) £74.00, c) £45.00, d) £40.80
Follow-up Activity: .pdf
Solutions: a) £17.10, b) £67.80

Contextual Area of a Triangle Using Sine
by Dave Taylor
Solutions: a) 5000kg, b) 4156.8kg, c) 3129.6kg, d) 4925.5kg
Follow-up Activity: .pdf
Solutions: a) 13522.96kg, b) 13950kg
by Dave Taylor
Solutions: a) 5000kg, b) 4156.8kg, c) 3129.6kg, d) 4925.5kg
Follow-up Activity: .pdf
Solutions: a) 13522.96kg, b) 13950kg

Contextual Volume of a Sphere
by Dave Taylor
Solutions: a) 7.82cm, b) 10.46cm, c) 8.77cm, d) 6.87cm
Follow-up Activity: .pdf
Solutions: a) 7.10cm, b) 8.56cm, 10.16cm
by Dave Taylor
Solutions: a) 7.82cm, b) 10.46cm, c) 8.77cm, d) 6.87cm
Follow-up Activity: .pdf
Solutions: a) 7.10cm, b) 8.56cm, 10.16cm

Density, Mass and Volume in Context
by Dave Taylor
Follow-up Activity: .pdf
Solutions: a) 49.8cm², b) 13.1g/cm³, c) 30.3
by Dave Taylor
Follow-up Activity: .pdf
Solutions: a) 49.8cm², b) 13.1g/cm³, c) 30.3

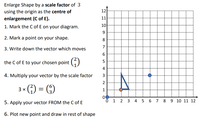
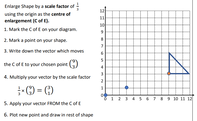
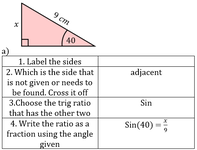
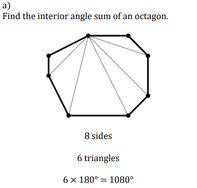
Interior Angle Sum of Polygons
by Dave Taylor
Solutions: a) 1080°, b) 1800°, c) 1440°, d) 1260°, e) 720°, f) 540°
by Dave Taylor
Solutions: a) 1080°, b) 1800°, c) 1440°, d) 1260°, e) 720°, f) 540°


Matrix Multiplication - Combinations of Transformations
by Dave Taylor
Solutions: a) A reflection in the line y = -x, b) A reflection in the y-axis, c) A reflection in the line y = x, d) A reflection in the x-axis
Follow-up Activity: .pdf
by Dave Taylor
Solutions: a) A reflection in the line y = -x, b) A reflection in the y-axis, c) A reflection in the line y = x, d) A reflection in the x-axis
Follow-up Activity: .pdf

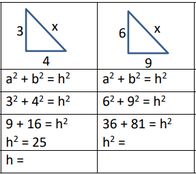
Pythagoras' Theorem - Calculating the Hypotenuse
by Alex Hughes
Solutions: a) 5, b) 10.82, c) 11.18, d) 13.89, e) 8.06, f) 6.32
by Alex Hughes
Solutions: a) 5, b) 10.82, c) 11.18, d) 13.89, e) 8.06, f) 6.32
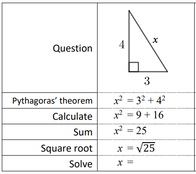
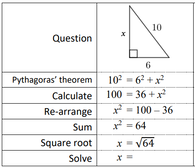
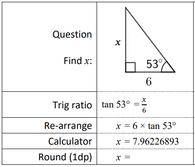
Right-Angled Trigonometry - Finding a Side Length, Unknown in the Numerator
by Simon Job
Solutions: .pdf
by Simon Job
Solutions: .pdf
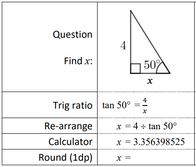
Right-Angled Trigonometry - Finding a Side Length, Unknown in the Denominator
by Simon Job
Solutions: .pdf
by Simon Job
Solutions: .pdf
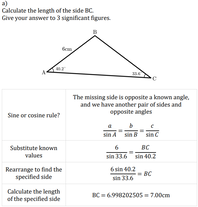
Sine or Cosine Rule
by Dave Taylor
Solutions: a) 7.00cm, b) 10.09cm, c) 3.61cm, d) 3.11cm
Follow-up Activity: .pdf
Solutions: a) 7.70cm, b) 5.21cm, c) 3.61cm
(All solutions given to two decimal places)
by Dave Taylor
Solutions: a) 7.00cm, b) 10.09cm, c) 3.61cm, d) 3.11cm
Follow-up Activity: .pdf
Solutions: a) 7.70cm, b) 5.21cm, c) 3.61cm
(All solutions given to two decimal places)

Speed, Distance and Time
by Dave Taylor
Solutions: a) 3.64m/s, b) 3.10m/s, c) 3.96m/s
(All given to two decimal places)
Follow-up Activity: .pdf
Solutions: a) 3.07m/s (to 2 d.p.), b) 40mph , c) 4:09
by Dave Taylor
Solutions: a) 3.64m/s, b) 3.10m/s, c) 3.96m/s
(All given to two decimal places)
Follow-up Activity: .pdf
Solutions: a) 3.07m/s (to 2 d.p.), b) 40mph , c) 4:09

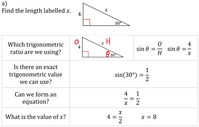
Using Exact Trigonometric Values
by Dave Taylor
Solutions: a) x = 8, b) x = 2, c) x = 4root(3), d) x = 16
by Dave Taylor
Solutions: a) x = 8, b) x = 2, c) x = 4root(3), d) x = 16
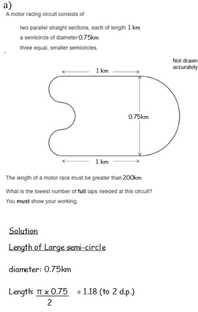

Vector Arithmetic
by Dave Taylor
Solutions: a) k = -9, b) k = -7, c) k = 3, d) k = 5
Follow-up Activity: .pdf
Solutions: a) k = -6, b) k = -3.5 , c) p = 1, r = -1
by Dave Taylor
Solutions: a) k = -9, b) k = -7, c) k = 3, d) k = 5
Follow-up Activity: .pdf
Solutions: a) k = -6, b) k = -3.5 , c) p = 1, r = -1

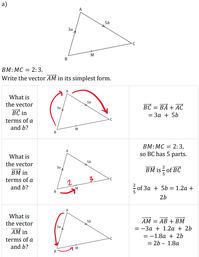
Vector Geometry (Ratios)
by Dave Taylor
Solutions: a) 2b - 1.8a, b) 4.8b - 0.4a, c) 3.75b - a, d) 3b - 3.2a
Follow-up Activity: .pdf
Solutions: a) 4.8b - 2a, b) 2.25c - a - 1.25b, c) 1.2a + 3b
by Dave Taylor
Solutions: a) 2b - 1.8a, b) 4.8b - 0.4a, c) 3.75b - a, d) 3b - 3.2a
Follow-up Activity: .pdf
Solutions: a) 4.8b - 2a, b) 2.25c - a - 1.25b, c) 1.2a + 3b

Volume of a Cuboid
by Dave Taylor
Solutions: a) 9.6cm, b) 6cm, c) 6.66666...cm, d) 3.75cm
Follow-up Activity: .pdf
Solutions: a) 12cm, b) 10cm from the top of the cuboid, in any position on any face or edge
by Dave Taylor
Solutions: a) 9.6cm, b) 6cm, c) 6.66666...cm, d) 3.75cm
Follow-up Activity: .pdf
Solutions: a) 12cm, b) 10cm from the top of the cuboid, in any position on any face or edge

Volume of a Cylinder
by Bob Jackson
Solutions: a) 502.7cm³, b) 565.5cm³, c) 1131.0cm³, d) 1570.8cm³, e) 377.0cm³, f) 15393.8cm³
by Bob Jackson
Solutions: a) 502.7cm³, b) 565.5cm³, c) 1131.0cm³, d) 1570.8cm³, e) 377.0cm³, f) 15393.8cm³

Volume of Pyramids and Spheres
by Dave Taylor
Solutions: a) 20.11cm, b) 32.17cm, c) 6.98cm, d) 19.88cm
Follow-up Activity: .pdf
Solutions: a) 24.43cm, b) 5.23cm, c) 5.86cm
by Dave Taylor
Solutions: a) 20.11cm, b) 32.17cm, c) 6.98cm, d) 19.88cm
Follow-up Activity: .pdf
Solutions: a) 24.43cm, b) 5.23cm, c) 5.86cm

STATISTICS AND PROBABILITY

Conditional Probability
by Dave Taylor
Solutions: a) 0.5625, b) 0.51, c) 0.788, d) 0.0975
Follow-up Activity: .pdf
Solutions: a) 0.75, b) 0.824, c) 53/150
by Dave Taylor
Solutions: a) 0.5625, b) 0.51, c) 0.788, d) 0.0975
Follow-up Activity: .pdf
Solutions: a) 0.75, b) 0.824, c) 53/150
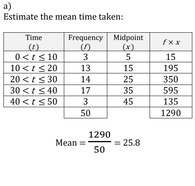
Estimating Mean From Grouped Data
by Dave Taylor
Solutions: a) 25.8, b) 27.75, c) 31.46, d) 35.4, e) 22.75, f) 46
by Dave Taylor
Solutions: a) 25.8, b) 27.75, c) 31.46, d) 35.4, e) 22.75, f) 46

Expected Value Using Probability
by Dave Taylor
Solutions: a) £80, b) £75, c) £31
Follow-up Activity: .pdf
Solutions: a) £110, b) £43
by Dave Taylor
Solutions: a) £80, b) £75, c) £31
Follow-up Activity: .pdf
Solutions: a) £110, b) £43

Mean Average - Missing Value Problems
by Dave Taylor
Solutions: a) 9, b) 88, c) 66, d) 69
Follow-up Activity: .pdf
Solutions: a) 7, b) 29, c) 42
by Dave Taylor
Solutions: a) 9, b) 88, c) 66, d) 69
Follow-up Activity: .pdf
Solutions: a) 7, b) 29, c) 42
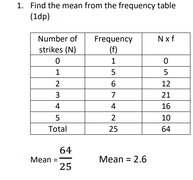
Mean of a Frequency Table
by Diana Page at Wootton Academy Trust
Solutions: .pdf
Follow-up Activity: .pdf
Solutions: .pdf
by Diana Page at Wootton Academy Trust
Solutions: .pdf
Follow-up Activity: .pdf
Solutions: .pdf

Mean of a Frequency Table (In Reverse)
by Dave Taylor
Solutions: a) x = 6, b) x = 15, c) x = 2, d) x = 5
by Dave Taylor
Solutions: a) x = 6, b) x = 15, c) x = 2, d) x = 5

Probability
by Dave Taylor
Solutions: a) 60, b) 56, c) 60, d) 48
Follow-up Activity: .pdf
Solutions: a) 60, b) 80, c) 100
by Dave Taylor
Solutions: a) 60, b) 56, c) 60, d) 48
Follow-up Activity: .pdf
Solutions: a) 60, b) 80, c) 100
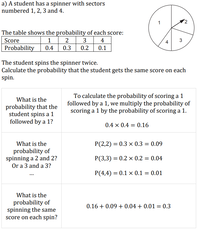
Probability of Successive Events
by Dave Taylor
Solutions: a) 0.3, b) 0.36, c) 0.425, d) 0.2946
Follow-up Activity: .pdf
Solutions: a) 0.315, b) 0.29, c) 1/6
by Dave Taylor
Solutions: a) 0.3, b) 0.36, c) 0.425, d) 0.2946
Follow-up Activity: .pdf
Solutions: a) 0.315, b) 0.29, c) 1/6

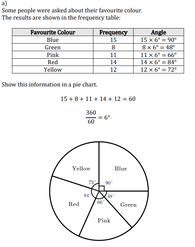

Tree Diagrams
by Dave Taylor
Solutions: a) 10/21, b) 16/33, c) 91/380, d) 60/119
Follow-up Activity: .pdf
Solutions: a) 51/100, b) 3 toffees and 7 mints, c) 2/15
by Dave Taylor
Solutions: a) 10/21, b) 16/33, c) 91/380, d) 60/119
Follow-up Activity: .pdf
Solutions: a) 51/100, b) 3 toffees and 7 mints, c) 2/15

Using Probabilities
by Dave Taylor
Solutions: a) 120, b) 90, c) 80, d) 30
Follow-up Activity: .pdf
Solutions: a) 60, b) 24, c) 40
by Dave Taylor
Solutions: a) 120, b) 90, c) 80, d) 30
Follow-up Activity: .pdf
Solutions: a) 60, b) 24, c) 40

Using Relative Frequencies
by Dave Taylor
Solutions: a) No (154), b) Yes (164), c) Yes (272), d) No (489)
by Dave Taylor
Solutions: a) No (154), b) Yes (164), c) Yes (272), d) No (489)

Venn Diagrams and Equations
by Dave Taylor
Solutions: .png
Follow-up Activity: .pdf
Solutions: a) 13/20, b) 19
by Dave Taylor
Solutions: .png
Follow-up Activity: .pdf
Solutions: a) 13/20, b) 19
